How many primes are there?

The prime numbers are one of those basic, yet mysterious, sets in mathematics, that while we know much about them, there are still many interesting open questions waiting to be answered, including probably the most well known conjecture in mathematics – the Riemann conjecture.

While this conjecture, and the attempts at its solution, use very advanced mathematics, even the most basic questions about the prime numbers already have many interesting results and lead to interesting tools, and in this post and the next two (here and here), we will try to understand some of these just by trying to “count” primes.

What is so special about primes?

The importance of prime number arise from the usefulness of integers in our daily (and mathematical) life. More specifically, multiplying numbers is very important, for example, computing area of a rectangle is the multiplication of its height and width, or if we have 5 cats and each meows 4 times a minute, then in an hour we will hear $5 \times 4 \times 60 = 1200$ meows.

Sometimes, we want to move at the other direction. For example, if we have a rectangle with integral sides and area 600, what can be its sides? What are all the ways to write $600= a\times b$ as integral decomposition? In general there can be many decomposition, but we might have a trick that can help us a lot. One simple decomposition is $600 = 60 \times 10$ , and both $10$ and $60$ are much smaller than $600$ , which can really help us. For example, we also know that $60 = 5 \times 12$ , which we can use to find another decomposition:

$600 = 60 \times 10 = (5 \times 12) \times 10 = 5 \times 120.$

Not only we can find more decomposition from just “understanding” these smaller numbers, but we can actually find all decompositions like that. And if you believe this claim, than you might have a good idea how to simplify your life even more. The number $10$ is smaller than $600$ , but we can even use the smaller numbers from the decomposition $10=2\times 5$ , or more generally:

The smaller the number, the better!

We can do the same for $60$ to get $60 = 2 \times 2 \times 3 \times 5$ . The numbers that we got stuck at, and could not decompose to smaller numbers are the prime numbers. In a sense, we want to have these three components:

Primes are the numbers that cannot be decomposed to “smaller” numbers.
Every number can be written as a product of prime numbers.
Once we understand one such decomposition, we understand all decompositions.

It seems reasonable, that for the right definition for (1), the decomposion in (2) holds. The claim in (3) is an interesting one and not trivial at all.

Some formalism:

Prime numbers have several definitions. The most prominent arises from the problem described above, and say that a number $p \notin \{-1,0,1\}$ is prime if it is only divisible by $\pm 1$ and $\pm p$ .

Another equivalent important definition, which leads to the 3rd part mentioned above, is as follows: If $p, a, b$ are any 3 integers, where $p$ divides $a$ or $b$ , then $p$ divides the product $ab$ . Using the notation $n \mid m$ for $n$ divides $m$ , this claim can be written as

$p\mid a \text{ or } p\mid b \;\Longrightarrow\; p \mid a\cdot b .$

Primes are then numbers $p\neq \{\pm 1\}$ where the converse holds as well, namely:

Definition: An integer $p\not \in \{-1, 0, 1\}$ is called prime if for any two integers $a, b$ we have:

$p\mid a \text{ or } p\mid b \iff p \mid a\cdot b .$

For example, for $p=2$ , saying that $2\mid a$ is what we call $a$ is even, and the primality of $2$ means that if $ab$ is even, then either $a$ or $b$ is even. And for a more specific example, $12$ is even and in each of the decompositions $12=2\cdot 6=3\cdot 4$ , at least one of the factors is even.

You should think of that definition as follows: if we know that a prime number $p$ divides some number, then no matter how we try to decompose that number, we will always see $p$ in that decomposition. This leads to the formal theorem of part (3) from above:

The Fundamental Theorem of Arithmetic:

Every integer $n$ can be written as a product of prime numbers, and more over, up to the plus\minus signs and the order of the primes, this product is unique.

To understand the uniqueness part above, consider the example of $n=6$ . There are four ways to write it as products of primes:

$6 = 2\cdot 3= 3\cdot 2= (-2) \cdot (-3) = (-3) \cdot (-2)$ .

While these are indeed 4 different ways to write the product, essentially we think of them as the same – we just choose the order of $2$ and $3$ , and choose their signs.

In particular, when restricting our attention to positive integers we get this equivalent result:

THEOREM: Let $P=\{ p_1, p_2, p_3, ... \} = \{ 2,3,5,7,... \}$ be the set of all primes, ordered in increasing manner. Then for any positive integer $n>0$ , there are unique nonnegative integers $\{k_1, k_2 ,k_3 ,... \}$ , almost all of which are zero, such that $n =\prod_i p_i^{k_i}$ .

Note that the fact that almost all of the $k_i$ are zero, implies that $n=\prod p_i^{k_i}$ is a finite product. When all the powers are zero, the product is $1$ and for our $n=6$ example from above, the product is $6 = 2^1 \cdot 3^1$ .

The integers is one of the most important sets out there, and the theorem above basically tells us that multiplicatively the prime are the building blocks of this set. To define an integer we only need to choose which primes are “in it” and how many times each of them appear. Now, that we know why the prime numbers are so important we can start asking basic questions about them, and the first question will be how many primes are out there?

A proof from the book

If we are given an integer $n$ , we can check if it is prime by simply going over all of $1<m<n$ and see if $m\mid n$ . In particular, if we want to count all the primes $<N$ we can do it in a finite amount of time (or aternatively, we can write a program and let a computer do it). But how can we count all of the primes, namely find the size of $P$ , and does it really have a finite size, or is it infinite? To answer this, it will take more than a simple prime counting algorithm.

In order to do this, Euclid found a very simple proof showing that there are infinitely many primes (and this was all the way back to around 300 BC !).

THEOREM: There are infinitely many primes

PROOF (Euclid) :

We start with any finite set of primes $\{p_1,...,p_k\}$ and we show that there are always other primes outside this set.

The idea is to use the relation between addition and multiplication inside the integers. The primes are defined multiplicatively, so we first multiply all of them to get a number which “contains” all of them, namely $n = \prod_1^k p_i$ . We then use the addition operation to “break” this property, and we claim that $n + 1$ isn’t divisible by any of these primes. Indeed, if $n + 1 = p_i\cdot m$ for some prime $p_i$ in our set and an integer $m$ , then

$1 = p_i\cdot m - n = p_i (m - \prod_{j\neq i }p_j)$ .

But $1$ is not divisible by numbers strictly larger than $1$ , and in particular prime numbers like $p_i$ .

Using the fact that every integer is a product of prime numbers, we know that there is some prime $q$ dividing $n+1$ , and it is not in $\{p_1,...,p_k\}$ , which is exactly want we wanted to show.

The distribution of primes

Now that we know that there are infinitely many primes, we can look for finer details about this set. Since its importance comes from its role inside the set of integers, we can ask how it looks as a subset. Let us start with the usual way people view the integers by writing them in the 10 columns we all know from elementary school, corresponding to the unit digit.

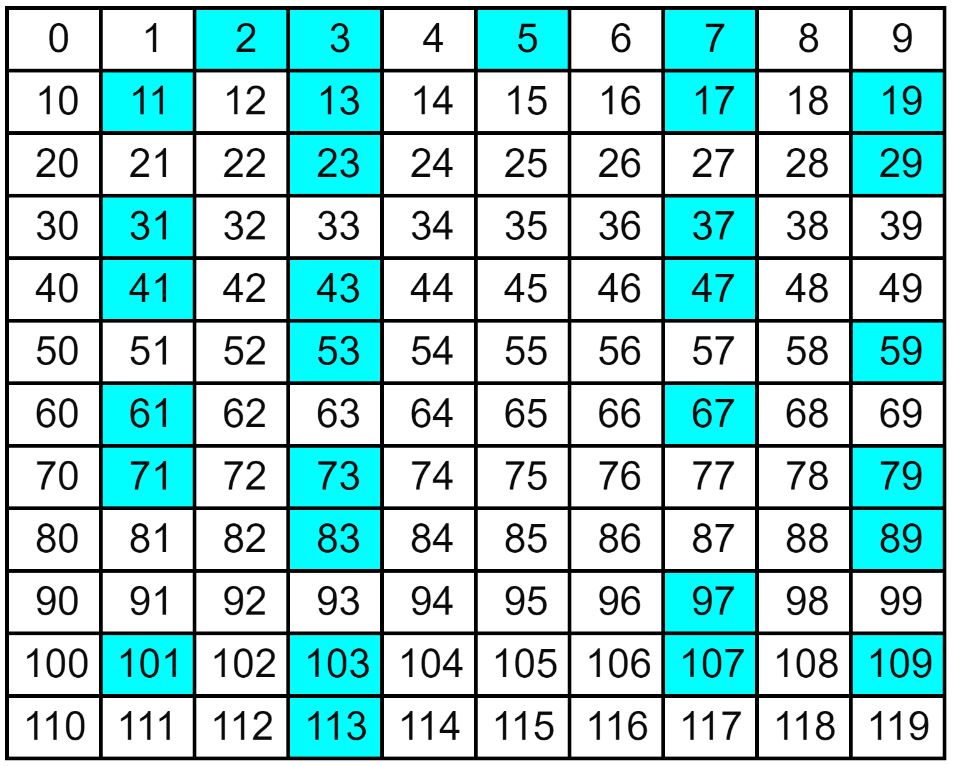
Just looking at this picture, we can already see (=conjecture!) some interesting phenomena.

The columns for the digits 0, 4, 6 and 8 don’t have any prime numbers.
The columns for the digits 2 and 5 have exactly one prime.
The columns for the digits 1, 3, 7 and 9 have a lot of primes – maybe infinite?
Also, if we look on a larger version of this table, it seems that the columns for 1, 3, 7, and 9 have the same number of primes.

The first two claims above are quite easy to prove. First we should note that the digits $0, 4, 6, 8$ and $2, 5$ from the first two claims above, are exactly those that have a non trivial common divisor with $10$ (which can be $2, 5$ or $10$ ).

Numbers which have a unit digit $d$ , are exactly those that we can write as $10\cdot k + d$ . If we assume that $d$ has a nontrivial common divisor with $10$ , for example if $d=2\cdot d_0$ is even, then the numbers with unit digit $d$ can be written as

$10\cdot k + d = 2\cdot 5 \cdot k + 2\cdot d_0 = 2 \cdot (5\cdot k + d_0).$

All of these numbers are divisible by 2, and by definition there is exactly one such (positive) prime – the number 2. So unless $k=0$ and $d_0=1$ , the number cannot be prime. In particular we get that the columns for $d=0, 4, 6, 8$ do not have any prime number, and the column for $d=2$ has exactly one prime. The same goes for the column with $d=5$ .

Here we used 10 columns because we are used to the 10 digit writing, but in general we can use any number $N$ of columns and ask if the $d$ ‘th column in it has zero or one prime. The same idea from above can be easily generalized to the following:

THEOREM: Let $N \geq 2$ be an integer and $0\leq d <N$ be another integer. If $N$ and $d$ have a nontrivial common divisor, then $\{N\cdot k + d \mid k \in \mathbb{N} \}$ contains exactly one prime if $d$ is prime, or zero primes otherwise.

Recall the we say that the numbers $a,b$ are equivalent mod $n$ and write $a \equiv b \;(mod \;N)$ , or $a\equiv_N b$ if they have the same remainder when divided by $N$ (or equivalently $N \mid (a-b)$ ). For example, saying that the unit digit of $n$ is 2, is the same as saying that $n\equiv_{10} 2$ . Also, two numbers are called coprime if they their greatest common divisor (gcd) is 1. With this notation, the theorem above can be written as:

THEOREM: Let $N \geq d\geq 2$ be integers which are not coprime. Then the number of primes $p$ such that $p \equiv_N d$ is either 1 if $d$ is prime and $0$ otherwise.

Our other two observations relate to the case where $N$ and $d$ are coprime, in which case we want to show that there are infinitely many primes, and there are more or less the same number is each of the columns. This first claim is usually known as Dirichlet’s theorem for prime numbers in arithmetic progression, and our final goal for these posts is to give most of the intuition and tools needed to prove it, and some intuition why the second claim holds as well.

Euclid’s proof revisited

Can we extend Euclid’s proof to show that there are infinitely many primes in the case of coprimality?

The simplest case is with $N=2$ and $d=1$ , or in other words we want to show that there are infinitely many odd primes. This is of course simple, because we already know that there are infinitely many primes and only one of them, $p=2$ , is even, so the rest are odd.

The first non trivial case is when $N=3$ and $d=1,2$ . Fixing, for example, $d=2$ , we can start as before with a finite set of primes $\{p_1, p_2, ..., p_k\}$ which are $2$ mod $N$ and consider the product $n = 1 + \prod_1^k p_i$ . There is still some prime $q$ which divides $n$ and it cannot be one of the $p_i$ , but unlike before, we don’t know that it also equals to $2$ mod $N$ . For example, for the first 3 such primes we get $1+ 2\cdot 5 \cdot 11 = 111 = 3\cdot 37$ , where $3 \equiv_3 0$ and $37 \equiv _3 1$ .

We already see that it becomes more complicated, but there is a trick that can help here. Consider instead the number $n = 3 \cdot \prod _1^k p_i -1$ . It is also easy to check that it is not divisible by any of the $p_i$ and by $3$ . It might still be divisible by only primes which are $1$ mod $3$ . Fortunately, we also get automatically that $n \equiv _3 2$ , and you can take it as an exercise to show that the product of numbers which are $1$ mod $3$ is also $1$ mod $3$ . Thus, we conclude that $n$ has at least one factor which is $2$ mode $3$ and it is not one of the $p_i$ , which is exactly what we wanted.

This trick is interesting in itself, and relates to the structure of the group of units mod $3$ (which I will not go into any further here), but already becomes much harder when trying to adapt it to the case of primes which are $1$ mod $3$ , not to mention when $N$ is larger. Furthermore, this type of proof doesn’t let us compare between the primes which are $1$ mod $3$ or $2$ mod $3$ . In order to do this next step we need to revisit the proof that there are infinitely many primes, but this time use Euler’s approach, and we shall do it in the next post.