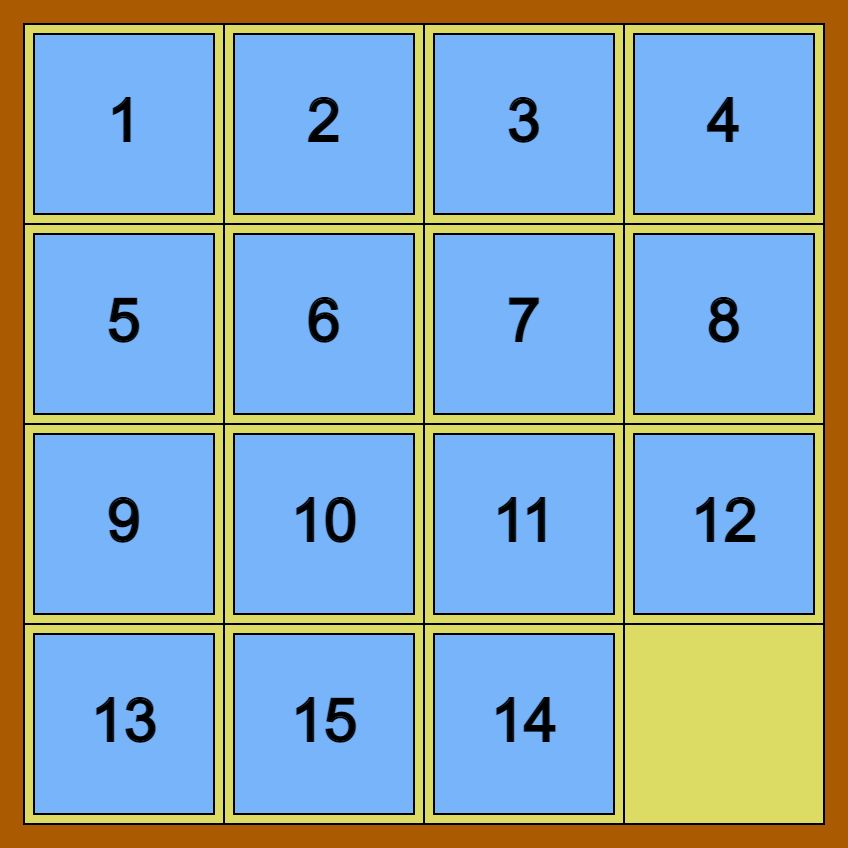
Almost 150 years ago the game 15-puzzle was invented and quickly gain lots of popularity. The rules are quite simple – you start with a $4\times 4$ board with 15 numbered pieces as in the image below, where the pieces are ordered according to their numbers, except the 14 and 15 pieces which switch positions. Given this board we are allowed to slide into the missing place any one of the pieces next to it, how many times that we want, and we win if we manage to get all the pieces in the right order.

This game became very popular during the 1880 and there was even a cash reward for anyone who can solve it. However, no matter how many people tried, no one could solve it, which is not surprising since it is unsolvable (what is surprising, it that it was proved to be unsolvable in 1879). Indeed – this game has a game invariant which doesn’t change when using legal moves and the initial state (with 14, 15 switched) and the ordered state have different invariants, so it cannot be solved.

In this post we will see, as mathematicians, how to even start thinking about this problem, and eventually get to this game invariant.

While this post is self contained, there is a more basic introduction to general game invariants in this and this post. For the Hebrew speaking readers, I made a video about this game here.

Finally, you can play the game yourselves here.

How to approach a problem

While we are going to give a full proof for the insolvability of the 15-puzzle, the main goal of this post is how to approach a problem, with this interesting problem as our example. I suggest that before you continue reading, you should try to play the game for some time, and see that you cannot actually solve it, and try reach some insights of your own and see eventually if they match the solution.

As for me, whenever I encounter a new problem, the first thing that I do to get some intuition is:

Find the simplest nontrivial example

Many times, we see a new problem and don’t even know where to start at. Which tools should we use, from which area? In this case, if we were just handed the game without any more information, we wouldn’t even know if we need to prove that it is solvable or not!

When there are too many variables and not enough information to know where to start, I usually try to simplify the problem as much as possible, without making it too trivial. Hopefully, we could then get some intuition which we can take with us to the original, more complicated problem.

In this case, to simplify the problem, we can take smaller boards instead of the $4 \times 4$ board. For a general board with $n$ places, we can add $n-1$ numbered pieces in the right order and then switch the last 2 pieces.

The simplest board is the $1\times 1$ board. However, this board will only have one empty place without any actual pieces, so it is also trivial. A board with 2 places will only have 1 numbered piece, so we didn’t even get to switch the last 2 pieces. To get to anything interesting, we need $n$ to be at least $3$ .

If the board is just one line, then it is still too trivial, since we can only move the piece back and forward, and this reason will not hold in the $4\times 4$ case.

With these trivial cases behind us, the first really nontrivial case is:

The $2\times 2$ board

Our first move will be to either move the “2” or the “3” piece. Suppose that we move “2”. The second move is to either move “2” or “1”. If we move “2”, then we are just going back to the initial state, so we will move “1”. In a sense, in this very simple case we have a “forward” and “backward” directions, which we can think of as moving the piece counter clockwise or clockwise. If we continue moving forward, namely moving “3” and then “2”, we will get to this state:

Note that again the missing piece is at the bottom right location. Another such rotation will produce

After one more such rotation, we will get back to our original state. It is now not hard to show that we have seen all the states that we can reach with legal moves. In particular, we didn’t reach the state with the pieces ordered, so this proves the insolvability for the $2\times 2$ board.

The question now, is can we say something that we might take with us to the $4 \times 4$ case? We have seen all the states that we can reach, meaning that we also know what are all the states that we can’t reach:

We can now observe a very interesting property of this $2\times 2$ game – exactly half of the states are reachable and half are not. Something like this usually means that there is some background structure to the problem that causes this half\half result. This structure might be true just for the $2\times 2$ or might be true in general. Before we try to prove it, let’s see if it holds in other small example.

The $3\times 3$ board

What does our new conjecture tells us in the $3\times 3$ case? We should try to figure out how many orderings our board may have, and hope to show that exactly half of them are reachable. However, in the $2\times 2$ case we had only $3$ pieces, and therefore only $3!=6$ orderings. In this case we have $8$ pieces and therefore $8!=40320$ orderings! This is much more that we can handle, and even a computer program will take some time running over all of these options. Luckily for us, we can also try our luck in smaller, non square boards.

The $2\times 3$ board

In the $2\times 3$ board, we have only $5$ pieces, so there are a total of $5!=120$ orderings, which is not that large. However, unlike our $2\times 2$ case, we no longer have the “forward” and “backward” directions. There are many ways to move the pieces to get to states where the missing piece is in the bottom right location.

This extra complication is problematic, but unlike having a whole new problem, it is just one more complication which we can deal on its own. The main problem was that there are a lot of ways for the “empty” piece to travel until it gets back to the bottom right location. However, if we don’t require it to return to its place, and only look at a single step, then it can only choose to move in at most four directions – up, down, left and right. This is a much simpler setting which we can track. However, simplifying this movement, we need to track more states of the board, since now the missing place can be everywhere. In other words, it is treated similar to the other pieces, so lets just add another piece labeled with “6” in the missing place, so that a legal move is to switch it with one of its neighbors:

The number of orderings is now $6!=720$ which is still not that large. Considering these orderings as vertices, and the legal moves as edges, we get a graph where the connected component of our initial state contains all the reachable states. Using any graph transversal algorithm will work here, and you can check that exactly $360$ states are reachable, and from those with the missing place at the bottom right corner exactly $60 = \frac{5!}{2}$ are reachable.

We now have an algorithm which can check our conjecture for us! You can even run it for the $3\times 3$ case, though it might take a while ( $9!$ is quite large). But for the $4\times 4$ case, the graph has size of $16! \sim 2\cdot 10^{13}$ , so I would advise against running the algorithm on it. However, now we have a conjecture and a starting place to understand our probelm:

Conjecture: Exactly half of the states are reachable.

With this conjecture, lets continue to the next step of trying to understand a problem.

Breaking the game

The easiest way to solve the game is to just take out all of the pieces, reorder them, and putting them back in. Or in other words – cheating. However, we just allowed ourselves to change the size of the board, so why not allow this also?

The idea of this step, is to allow ourselves to break the game to a degree and try to move from rules which allow us to solve the game to rules which don’t allow us to solve, and hope that we find where these good and bad rules meet and somehow get some intuition about the game along the way.

Note that in a sense this step is very similar to the previous step. We try to move a long a spectrum of parameters (in the previous step it was the board size, and here they are the rules), where at one endpoint we know exactly what happens, and we try to reach the second endpoint with some conjectures or results along the way.

In our game, one endpoint is the standard rules of “moving” the missing piece, while at the other endpoint we allow to change the order completely, which of course makes the game solvable. However, even if “break” it a bit less, and we only allow to switch between any two pieces, it is enough to solve the game, since we only need to switch 14 and 15 (or in general the last two numbered pieces). These are much simpler rules than being able to do anything, so it is much easier to work with them. However, you should try to show that these simpler rules are actually enough to get to any ordering. This result is not that important here, but it gives a better view of our problem, and is connected a bit to the final step of the proof.

In the standard rules, we can also switch between two pieces, but have extra conditions. The first is that one of the pieces is the “missing” piece, or the “16” piece. The second is that we can only move up, down, left or right. If we delete the second restriction – namely the rules are that we can switch “16” with any other piece, then it is quite easy to see that the game is solvable. This means that there is something important in the up\down\left\right movement that makes the game unsolvable.

Thinking about it for a few minutes, one observation comes to mind. Since “16” starts and end in the bottom right corner, for every time it moves up it needs to move also down eventually, and similarly with the left\right movement. In particular, this means that we move an even amount of steps. We can also see it by coloring our board by red and blue alternatively as follows:

To return the missing piece to the bottom right, we must do even amount of steps

The “16” piece starts at red, and ends in red, and since at each step it changes colors, at must make even amount of steps.

This observation connects to our previous observation. If we must have even amount of steps, then it sounds reasonable that half of the state will be reachable (for even amount of steps) and half not reachable (odd amount). Moreover, to check the importance of this observation, we can try to look at the rules where we are allowed even amount to switching between any two pieces (not necessarily with “16”). If you try it with the smaller boards, you will see that you get exactly the same reachable states as with the standard rules – so this parity condition must be really important.

At this point, we have two interesting, probably connected observations (still not proved for a general board):

Legal games have even amount of switching between any two pieces.
Exactly half of the states are reachable.

If you already studied some group theory, then a couple of lightbulbs should have light up around you. This sounds very similar to the parity of a permutation, and indeed, this will be the final step.

The symmetric group and the even permutations

Up until now we talked about ordering of our pieces, with or without the missing piece. The structure used to study this sorts of object is called the symmetric group. The symmetric group $S_n$ is the group of all permutation on $n$ elements. In this post we will assume familiarity with the symmetric group (though let me know if you want a separate post explaining it), and we start by recalling the basic results needed for us.

Recall first that if $\sigma\in S_n$ is any permutation, then we can write it as a product of disjoint cycles. For example, the permutation

can be written as $(1\; 3\; 6)(4\; 5)(2)$ . Most of the times, we don’t write the 1-cycles and simply write $(1\; 3\; 6)(4\; 5)$ instead.

A single 2-cycle, namely $(i\; j)$ where $i\neq j$ is called a transposition. One of the first result that we learn about the symmetric group is that

Theorem: Every permutation can be written as a product of transpositions. In other words, the transpositions generate the symmetric group.

This is not a hard theorem to prove. Simply think of getting a mixed deck of cards that you want to order. To get the ace of hearts to the top of the deck, you only need to switch with the card at the top of the deck. You can then switch the 2 of hearts card with the card just below the top of the deck and so on.

In our puzzle world, we have a set of 16 pieces (including the missing one) and an initial state which can represented as the permutation $(14\; 15)$ . We then ask if we can get it using transpositions, each including 16 and one of its neighbors. However, we later saw that we can allow any transpositions, as long as it is an even amount. In other words, we asked if we can write

$\displaystyle{(14\; 15) = \prod_1^{2m} \tau_i\;\;,\;\; \tau_i \text{ are transpositions}}.$

The goal is to show that when writing a permutation as a product of transpositions, the parity of the number of transpositions is well defined. This means that in the equation above the left hand side is an odd permutation, while the right hand side is an even permutation, and therefore there is no solution.

What are even permutations

We already know that each permutation can be written as a product of transpositions. We now want to extend this result and show that while the number of transpositions in this presentation is not uniquely determined the parity of this number is.

Start with examples

As before, when trying to understand a new object, we start with the simplest nontrivial example that we can find, which in this case is where the permutations are of $n=2$ elements $\{1, 2\}$ . In this case there is exactly one permutation which can be written with 0 transpositions, namely the identity, and exactly one permutation which can be written with 1 transposition, namely the transposition $(1\; 2)$ . This already covers all the permutations, so we can write

$EVEN_2 = \{id\}\;\;\;,\;\;\; ODD_2 = \{(1\; 2)\}$

and try to show that these are really the even and odd permutations. The proof here is not too difficult, because we only have one transposition $(1\; 2)$ and $(1\; 2)^k$ is either the identity if $k$ is even or $(1\; 2)$ if it is odd.

For permutations on $n=3$ , it becomes a little bit trickier to prove, since we have 3 transpositions. First, to find our candidates for the even and odd permutations, you can check that the identity is the only product of 0 transpositions, the 3 transpositions $(1\; 2), (1\; 3)$ and $(2\; 3)$ are the only products of 1 transpositions, and finally the identity and the two 3-cycles $(1\; 2\; 3)$ and $(1\; 3\; 2)$ are the products of 2 transpositions. We already saw all of the permutations, so we would like to show that

$EVEN_3 = \{Id, (1\; 2\; 3), (1\; 3 \;2)\}\;\;\;,\;\;\; ODD_3 = \{(1\; 2), (2\; 3), (1\; 3)\}$

are the even and odd permutations respectively.

Since we have 3 transpositions, it is not as straight forward as with the $n=2$ , but it is still not difficult. We just need to show that any element in $EVEN_3$ when multiplied by a transposition is going to be in $OOD_3$ and similarly the other way around. Since $|EVEN_3| = 3$ and there are $3$ transpositions, there are $9=3\times 3$ computations that we need to do, and an extra $9$ computations for the other direction. As an exercise, show that because each transposition is its own inverse, you can get the second batch of $9$ computations for free.

At least for when multiplying by the transposition from the right you get the following diagram:

Connecting the permutations by multiplying by transpositions. The red, green and blue edges correspond to multiplying by (1 2), (1 3) and (2 3) respectively.

As another exercise, show that it is enough to consider the right multiplication.

You can do the same for $n=4$ and get that $EVEN_4$ contains the (1) identity, (2) 3-cycles (there are 8 such permutation) and (3) product of two disjoint transpositions (3 permutations), while $ODD_4$ are the (1) single transpositions (6 permutations) and (2) 4-cycles (6 permutations). Or written generically

$EVEN_4 = \{id, \;(i\; j\; k),\; (a\;b)(c\;d)\} \;\;\;,\;\;\; ODD_4 = \{(i\;j),\; (a\;b\;c\;d)\}$

Now comes the hard part. We need to somehow characterize the sets $EVEN_n$ and $ODD_n$ for general $n$ . Once they are properly defined, we need to show that multiplying by transpositions moves us from one set to the other.

Next we generalize

One property that can be seen in our simple examples, is that the parity of a permutation doesn’t change when we relabel the elements, or more precisely two permutations with the same cycle structure have the same parity. For example, if one 3-cycle is an even permutation, then all 3-cycles are even permutations. Another example, which you can check in $n=5$ is that $(1\; 2\; 3)(4\; 5)$ is an odd permutation, and by our conjecture all the products of disjoint 3-cycle with 2-cycle are odd (for example $(1\; 5\; 2)(3 \;4)$ ). You should take it as an exercise to show that if the parity is well defined, then it must have this property. For now, lets try to use this conjecture and maybe get some intuition on how to prove the general claim.

With this maybe a clue, lets ask what happens to the cycle structure when multiplying by a transposition. In our example above we only had very simple structure, since $n$ was very small, so at this point you should start with some random permutation for some large $n$ with a lot of disjoint cycles and see what happens there when multiplying by the different transpositions. If you run a few examples like this, you will see something interesting:

Conjecture: When multiplying a permutation given as product of disjoint cycles with a transposition – either one cycle splits into two cycles, or two cycles are combined into one.

Once we have this conjecture from our experiments, it is an easy exercise to actually show it, and I will leave it as such.

Assuming this claim, let’s show how to complete our proof. While we don’t know if the parity of the number of transpositions is well defined, the number of disjoint cycles appearing in a permutation is well defined, and therefore its parity is well defined. For example, in our $EVEN_4$ case above we had the identity $id = (1)(2)(3)(4)$ the 3-cycles (e.g. $(1 \;2\; 3)(4)$ ) and the product of disjoint 2-cycles (e.g. $(1 \;2)(3 \;4)$ ) and they all have even number of cycles (4 or 2). Similarly all the permutations in $ODD_4$ have odd number of cycles (3 or 1). The same happens in $EVEN_3$ and $ODD_3$ , but notice that there the permutations in $EVEN_3$ have odd number of disjoint cycles while $ODD_3$ have even amount.

More generally, we can re(well)define these sets for general $n$ as follows. If $|\sigma|$ is the number of disjoint cycles in $\sigma$ , then

$EVEN_n = \{ \sigma : |\sigma|\equiv_2 n \}$

$ODD_n = \{ \sigma : |\sigma|\equiv_2 n+1 \}$ .

Other than the fact that these are well defined, what other properties do these sets have? Since every permutation has either even or odd amount of disjoint cycles, then $S_n = EVEN_n \sqcup ODD_n$ , and in particular $id\in EVEN_n$ since the identity has $n$ cycles (of size 1) in $S_n$ . Moreover, by the exercise above, if $\tau$ is a transposition then $\tau \cdot EVEN_n \subseteq ODD_n$ and $\tau \cdot ODD_n \subseteq EVEN_n$ . Actually, because $\tau^2=id$ these are equalities (and in particular $|EVEN_n|=|ODD_n|$ ).

Finally, a simple induction shows that a product of even (resp. odd) amount of transpositions is in $EVEN_n$ (resp $ODD_n$ ), which is exactly what we wanted to show.

Even permutation are reachable

At this point we know that legal moves can only create even permutations (when the missing piece returns to the bottom right corner). However, is the opposite true as well? Given any even permutation, can we generate it using legal moves? In this section we will give the main ideas which can be used to show that for boards with at least two rows and two columns this is true.

We have already used the fact that every permutation can be written as a product of transpositions. A bit less known, but still not that hard, is the fact that all even permutation can be written as a product of 3 cycles.

Claim: Every even permutation is a product of 3-cycles.

Proof: Any even permutation can be written as a product of even number of transpositions. Thus, it is enough to prove this claim for a product of two transposition, and this is left as an exercise.

Going back to our $n\times m$ puzzle, with $n,m\geq 2$ , we want to show that any 3-cycle can be generated using legal moves.

There are certain 3-cycles which are really easy to generate on our board. These are the cycles which contain a piece, its right neighbor and its bottom neighbor. For example, the $5, 6, 9$ pieces in the $4\times 4$ board can be cycled as follows:

These already generate a lot of 3-cycles – denote the set of all these cycles by $T$ . We claim that these already generate all of the even permutations. The main idea is to use conjugation since $\sigma (a\; b\; c) \sigma^{-1} = (\sigma(a)\;\sigma(b)\;\sigma(c))$ – a conjugation of a 3-cycle is another 3-cycle.

Lets see as example how to show that the 3-cycle $(2\;6\;10)$ is in the group generated by $T$ .

Using the $\sigma_1=(1\;2\;5)\in T$ , it is enough to show that $\sigma_1 (2\;6\;10) \sigma_1^{-1} = (5\; 6\; 10)$ is in the group generated by $T$ . Note that this cycle no longer change any element in the top line.
Next, using conjugation by $\sigma_2=(9\;10\;13)$ , we can look at $(5\;6\;13)=\sigma_2(5\;6\;10)\sigma_2^{-1}$ .
Finally, $(5\;6\;13)$ is in $T$ so we are done.

I will leave the general induction process for any 3-cycle and any board as an exercise.

In conclusion – what did we see?

We started with a new problem without knowing too much about it. Looking for ways to investigate it, we tried to look for simpler versions of the problem where we can solve it. Once we had such a version, we added back the complexity a bit by bit, each time trying to understand only this new complexity and looking for observations which might help to understand the original problem. In this case we saw that not only the game is not solvable, but half of the initial states are not solvable.

We did a similar process by changing the rules of the problem – also moving from a simple version to the complicated one. Looking for all sorts of rules is much more difficult, since there can be so many of them. However, since we already had this half\half observation, it was easier to focus on a certain rule about the parity of the number of steps.

By that time we had in our hands an almost mathematical conjecture, which led to a well known result about the symmetric group. Even when trying to understand this result, we were able to use similar approaches to solve it.

Hopefully by now you see how powerful these simple steps can be. They can be applied to new and complicated problems, as well as homework problems. Once we have a solution and a lot of intuition about a given problem, we can start to look for more elegant and hopefully shorter solutions.

The 15-Puzzle and the symmetric group

How to approach a problem