Complex Analysis – Lecture notes (Hebrew)

  1. Introduction – why do we need complex numbers
  2. The field of complex numbers
  3. Continuity and derivatives
  4. The Cauchy Riemann equations
  5. Elementary functions
  6. Complex integrals
  7. Cauchy’s formula
  8. Applications of Cauchy’s formula (Average, Maximum principal and Lioville’s theorem)
  9. Infinite sums of functions
  10. Taylor and Laurent expansions
  11. Singularities
  12. The residue theorem
  13. Computing real integrals
  14. And even more real integrals

Some complex visualizations:

When trying to visualize real functions f:\mathbb{R}\to\mathbb{R}, we usually look at their graph, which is a 1-dimensional object in the 2-dimensional plane.
When considering complex functions g:\mathbb{C}\to\mathbb{C}, we suddenly need to view a 2-dimensional surface in a 4-dimensional world \mathbb{C}\times \mathbb{C} \cong \mathbb{R}^4.

This is not so easy to do in our 3-dimensional world (not to mention our 2-dimensional screens). However, there are few ways to view complex number, giving us some glimpses about the nature of such functions.

Two copies of the plane:

One way to view our complex function, is to just have two copies of the complex plane, and show on one size a point z and on the other copy the point g(z). For example consider the function g(z)=\exp(z):

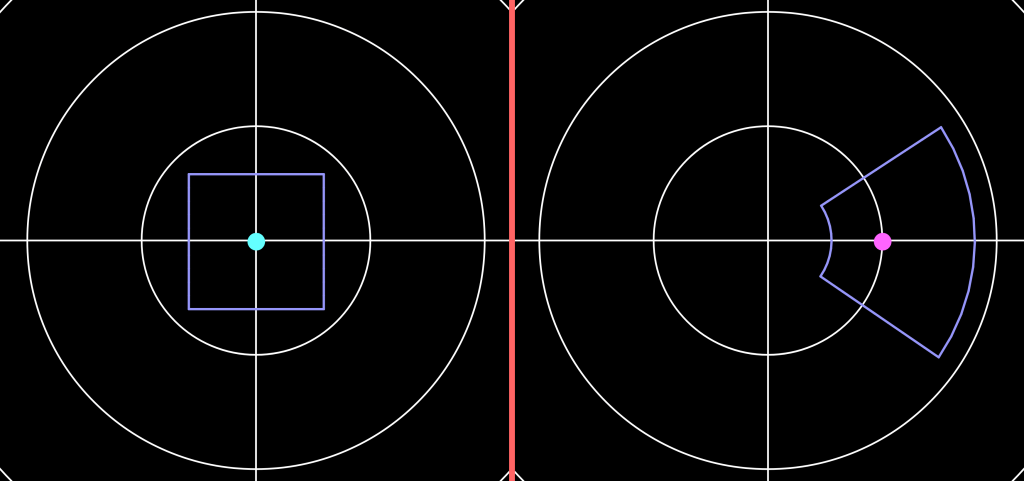
On the left we have the teal point at the origin, and a purple square around it. Since \exp(0)=1, the central point is mapped to 1, which is the pink point. Horizontal lines are mapped by the exponent function to rays coming out of the origin, and vertical lines to circles (See the elementary function lecture notes for more details). This means that the square transforms into the purple shape on the right.

To view more such examples, with more elementary functions, go to:
https://openprocessing.org/sketch/1811203
In particular check out the simpler functions like g(z)=z^2 which have several nice properties which can be viewed using this method, however, it is less obvious with a static image than with an interactive program.

Complex numbers as vectors:

The simplest visualization of a complex function g:\mathbb{C}\to\mathbb{C}, is at each point z\in \mathbb{C}, to view its image g(z)\in \mathbb{C} as a 2d-vector. Drawing these vector for a lattice of points on the plane produces such images:

  1. On the left: The identity function g(z)=z. This means that the arrow at point z is at direction z, namely it is radially out, and the bigger |z| is, the bigger the arrow.
  2. On the middle: The function g(z)=z^2. Note that for example, when z\in\mathbb{R} is real, its square z^2 is always positive, so that the arrow must point to the right. Similarly, when z=ri is pure imaginary, its square is z^2 = -r^2 is negative, so that the arrow points to the left.
  3. On the right: The function g(z)=z^2-1. This function has two roots at z=\pm 1, which we can see as a pulling and pushing point in the image.

To check out more examples, go to:
https://openprocessing.org/sketch/1246491

Also, considering it as a flow field, you can view it dynamics here:
https://openprocessing.org/sketch/1244668

Complex numbers as colors:

Another interesting way to view complex number is by using their polar presentation z=r\cdot e^{i\theta}. We can use this presentation to choose a color using the HSB (Hue, Saturation, Brightness) color system, and color the point z in the plane using the corresponding color for g(z).
More specifically, the color correspondence is according to following image:

  • The radius r parameter controls the brightness. Near the origin the color is darker up to full black at the origin, and farther away it is more bright (more colorful).
  • The argument \theta parameter controls the hue. As we rotate around the origin we see all the different colors, and in particular teal is for positive numbers, red is for negative, and similarly green\yellow for ri with r>0 and purple\blue for r<0.

For example, consider the functions g(z)=z^2-c for some constant c, where we add extra black lines to see where |g(z)| passes through the integers.

  1. On the left: g(z)=z^2-1. We see the two roots at \pm 1 as the black points. Between them the function is negative (e.g. g(0)=-1) so the color is red. On their right and left over the real line the parabola is positive, so it has teal color.
    Note that when we go around each of the roots, we see all the color, and at the same order.
  2. On the middle: g(z)=z^2. It has a single double root, which is the big black point in the middle. More over, when going around it we see each color twice, indicating that it is a root of order 2.
  3. On the right: g(z)=z^2+1. Similar to the z^2-1 example, but with two roots at \pm i. Note that this function is positive on the real line, or in the color presentation it only has the teal color there.

To check out more examples, go to:
https://openprocessing.org/sketch/1246306