Math Visualization Portfolio

Triangle group tiling

Start with one triangle and take its reflections through each of its edges. Then for each reflection, take its reflection through each of its edges (one of them will be the original triangle). Continue like this until you cover the whole plane.

In general, these triangles will intersect one another, but sometimes, some magic happens, and everything falls into place nicely, and along the way produces interesting images in three different geometries – Euclidean, Spherical and Hyperbolic.

• Euclidean geometry – Shadertoy
• Spherical geometry – Shadertoy
• Hyperbolic geometry – Shadertoy
• All together in openprocessing
• Explanatory video (Hebrew)
• Explanatory video (English)

Matrix action on Poisson disc

Number theory stands at the heart of mathematics, and there are many ways of studying it. One way is to look for interesting dynamical processes describe in this number theoretic world. In particular, one of the simplest and basic such dynamics is with the simple continued fractions. Its continuous extension, leads to the space of lattices and its geometry, and also to many interesting visualizations.

• Matrix action on the disc – Openprocessing

Julia Set

Given a function , what happen if we take some starting point and see what happens if we apply to it again and again and again ?

Other than the mathematics behind this interesting dynamical system, it also has a beautiful visualization. Simply color each point according to “how fast” it goes to infinity, to obtain amazing fractal images

Julia Set – Openprocessing

Riemann Sphere

We all know the standard real plane, and we all know how infinite it can sometimes be. Not only that, you can go to infinity in many directions. But what if we take all this infinities and combine them all to a single point? This interesting idea is manifested in the stereographical projection from the Riemann sphere onto the plane.

• Riemann Sphere – Shadertoy
• Short video

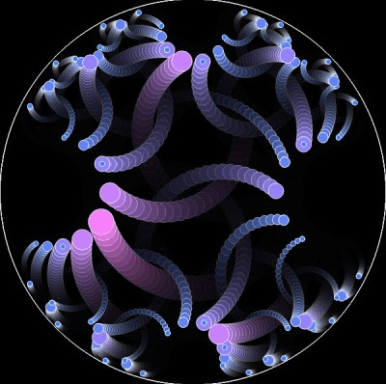
Cayley graph of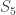

The family of symmetric groups is one of the basic building block of group theory and therefore of mathematics. As such, it is always interesting finding new ways of understanding and visualizing them. Up to the group $S_n$ is “relatively” simple, but at $n=5$ it becomes “complicated” simple. Trying to understand it using its standard Cayley graph visualization leaves us with 5-dimensions to follow which is not easy. However, with some simple math tricks, we can lower the dimension to 3, producing this interesting result.

Cayley graph of – Shadertoy

Algebraic integers

The integers are the most basic numbers that we use on our daily lives. The nonnegative counting integers 0,1,2,… and their negatives -1,-2,… . Extending this system, e.g. to rational, real and complex numbers, is the basis of most of our current science.

Another very important such family are the algebraic integers. These are exactly the roots of monic polynomials with integer coefficients. For example is a root of such a polynomial . These have many interesting properties, and at least one of them is how they are arranged in the plane. In particular, plotting them according to the degree and size of the coefficients give us this interesting image.

• Algebraic integers – Openprocessing
• Short video

Truchet Tiling

Tiling the plane with interesting tiles is a fascinating way of creating interesting patterns. One such type of tiling, is by using the same tile shapes (e.g. square, triangle) but with different patterns on that shape. Then when you rotate the patterns on each tile you get more and more patterns.

Here are several such example with different tile shapes and patterns.

• Open processing curation
• Squares Truchet + Open processing tutorial
• Squares with different sizes
• Leaf triangles
• Squares and octagons
• Triangles and hexagons (Magen David)
• Rotating maze

Voronoi Tiling

Another way to tile the plane, is by randomly choosing some special points in the plane, and for each one define the cell of all the points in the plane which are nearer to it than to other special point.

Playing around with the location of these special points, or the distance function itself, leads to all sort of interesting tilings of the plane.ns.

• Standard Voronoi tiling – Openprocessing
• Voronoi stones (rounded corners) – Openprocessing
• Voronoi spider web – Openprocessing

Possible to impossible games

There are some games which seem impossible to beat (I am looking at you Spelunky), but enough hard work and dedication will let you be victorious at the end.

However, sometimes, maybe with a slight variation, these games can be mathematically proven to be impossible to beat. Here are a few, plus some posts I wrote about them:

• The 15 puzzle (Openprocessing), and corresponding post.
• Peg solitaire (Openprocessing), and corresponding post.
• Rubik’s cube (Openprocessing)

Cave exploration

Using interesting mathematics and algorithms like ray marching and natural noise to create this cave exploration experience.

• Cave exploration – Shadertoy
• Explanatory video (Hebrew)

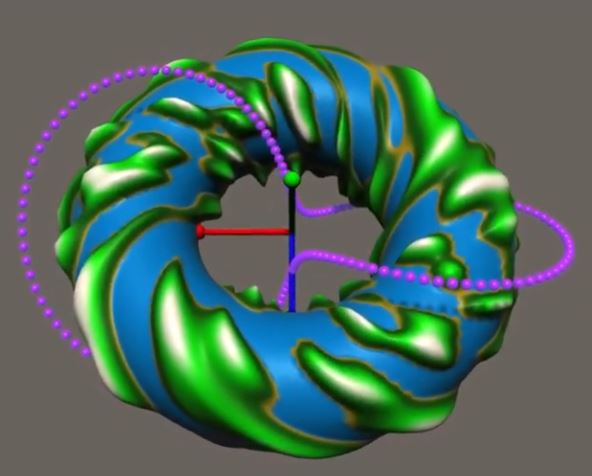
Dehn Twist

If I cut a piece of cloth, but then sew it back together exactly where it was cut and its looks “the same”, is it really? Are there differences which we can measure between the before and after of this process? Formalizing this type of questions and trying to answer them is one of the goal in the study of topology. In particular, an interesting example of this cut and sew (glue) process is the Dehn twist where we cut a torus (doughnut) and sew it back, but not exactly “the same”…

• Short video